2.2. 时域中的离散时间系统¶

在时域中，离散时间系统对输入信号或者延迟信号进行简单运算处理，生成具有所需特性的输出信号。本节的目的就是通过Python仿真一些简单的离散时间系统，并研究它们的时域性质。

离散时间系统¶

本课程中，我们主要研究的线性时不变离散时间系统，形式如下的线性常系数差分方程来描述。

\[\sum _ { k = 0 } ^ { N } d _ { k } y [ n - k ] = \sum _ { k = 0 } ^ { M } p _ { k } x [ n - k ]\]

其中，\(x[n]\)和\(y[n]\)分别是系统的输入和输出，\(d[k]\)\(p[k]\)为常数，离散时间系统的阶数为\(\max(N,M)\)，表示系统差分方程的阶数。

若系统是因果的，还可以进一步将上述形式化简

\[y [ n ] = - \sum _ { k = 1 } ^ { N } \frac { d _ { k } } { d _ { 0 } } y [ n - k ] + \sum _ { k = 0 } ^ { M } \frac { p _ { k } } { d _ { 0 } } x [ n - k ]\]

已知\(x[n]\)和初始条件\(y[n_0-1],y[n_0-2],\cdots,y[n_0-N]\)，那么可以计算出\(y[n]\)。

利用Scipy包来对系统进行仿真

scipy.signal.lfilter(b, a, x, axis=-1, zi=None)

其中，\(b\) 和 \(a\)分别为系统差分方程的系数

\[a[0]y[n] = b[0]x[n] + b[1]x[n-1] + ... + b[M]x[n-M] - a[1]y[n-1] - ... - a[N]y[n-N]\]

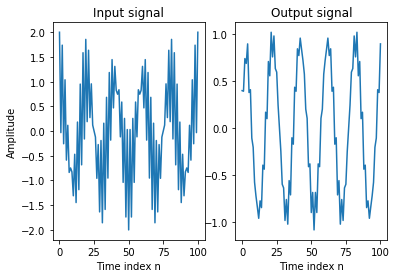
例：滑动平均系统¶

\[y [ n ] = \frac { 1 } { M } \sum _ { k = 0 } ^ { M - 1 } x [ n - k ]\]

通过若干个正弦信号之和所组成的信号中滤除高频分量

[9]:

# 加载所需要的包
import matplotlib.pyplot as plt
from scipy import signal
import numpy as np
# 产生两个不同频率正弦序列
n = np.linspace(0,100,101)
s1 = np.cos(2*np.pi*0.05*n) # 信号1
s2 = np.cos(2*np.pi*0.47*n) # 信号2
x = s1+s2

# 平滑滤波处理
M = 5
b = np.ones([M,])
y = signal.lfilter(b,np.array([1,0,0]),x)/M

# 显示结果
plt.subplot(121)
plt.plot(n,x)
plt.ylabel('Amplitude')
plt.title('Input signal')
plt.xlabel('Time index n')

plt.subplot(122)
plt.plot(n,y)
plt.title('Output signal')
plt.xlabel('Time index n')
plt.show()

../_images/experiments_dt_systems_1_0.png

线性系统和非线性系统¶

对于线性离散时间系统，若\(y_1[n]\)和\(y_2[n]\)分别是输入序列\(x_1[n]\)和\(x_2[n]\)的响应，则输入为

\[x[n] = \alpha x_1[n] +\beta x_2[n]\]

的输出响应为

\[y[n] = \alpha y_1[n] +\beta y_2[n]\]

上式的叠加性质对于任意常量\(\alpha\)和\(\beta\)以及任意输入\(x_1[n]\)和\(x_2[n]\)都成立。

若存在一组非零的\(\alpha\)和\(\beta\)，或者一组非零的输入序列\(x_1[n]\)和\(x_2[n]\)，上述叠加性质不成立，则系统为非线性系统。

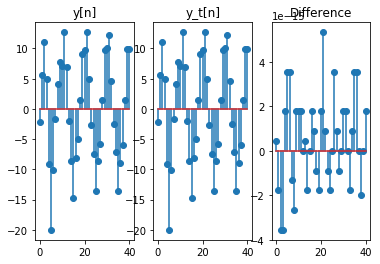
现在我们来研究下面这个系统的线性性质，

\[y [ n ] - 0.4 y [ n - 1 ] + 0.75 y [ n - 2 ] = 2.2403 x [ n ] + 2.4908 x [ n - 1 ] + 2.2403 x [ n - 2 ]\]

[2]:

# 产生混合信号：高频正弦+低频正弦
n = np.linspace(0,40,41)
s1 = np.cos(2*np.pi*0.1*n)
s2 = np.cos(2*np.pi*0.4*n)
a = 2
b = -3
x = a*s1+b*s2

# 定义系统的系数
num = np.array([2.2403,2.4908,2.2403])
den = np.array([1,-0.4,0.75])

# 系统处理（滤波）
ic = np.array([0,0]) # set initial
zi = signal.lfilter_zi(num, den)
y1,_ = signal.lfilter(num,den,s1,zi=zi*ic) # y1[n]
y2,_ = signal.lfilter(num,den,s2,zi=zi*ic) # y2[n]
y,_ = signal.lfilter(num,den,x,zi=zi*ic)   # y[n]
yt = a*y1 + b * y2

# 计算叠加输入的响应和输出直接叠加的差异
d = y-yt


plt.subplot(131)
plt.stem(n,y)
plt.title('y[n]')
plt.subplot(132)
plt.stem(n,yt)
plt.title('y_t[n]')
plt.subplot(133)
plt.stem(n,d)
plt.title('Difference')
plt.show()

../_images/experiments_dt_systems_3_0.png

时不变系统和时变系统¶

对于离散时不变系统，若\(y_1[n]\)是\(x_1[n]\)的响应，则输入

\[x[n] = x_1[n-n_0]\]

的输出为

\[y[n] = y_1[n-n_0]\]

其中\(n_0\)是任意整数。上面的输入输出关系，对任意输入序列及相应的输出成立。

若对至少一个输入序列及其相应的输出序列不成立，则称系统为时变的。

例子¶

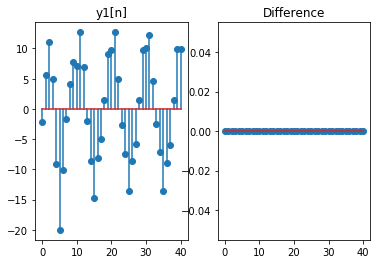
验证如下系统是否为时不变：

\[y [ n ] - 0.4 y [ n - 1 ] + 0.75 y [ n - 2 ] = 2.2403 x [ n ] + 2.4908 x [ n - 1 ] + 2.2403 x [ n - 2 ]\]

我们产生两个不同的输入序列\(x[n]\)和\(x[n-D]\)，计算出相应的输出序列\(y_1[n]\)和\(y_2[n]\)，以及二者的差\(d[n]=y1[n]-y2[n+D]\)，若\(d[n]\)为0，则系统是时不变的。

[3]:

# 产生混合信号：高频正弦+低频正弦
n = np.linspace(0,40,41)
a = 2
b = -3
D = 10
x = a*np.cos(2*np.pi*0.1*n)+b*np.cos(2*np.pi*0.4*n)
xd = np.concatenate((np.zeros([D,]),x),axis=0)


# 定义系统的系数
num = np.array([2.2403,2.4908,2.2403])
den = np.array([1,-0.4,0.75])

# 系统处理（滤波）
ic = np.array([0,0]) # set initial
zi = signal.lfilter_zi(num, den)
y1,_ = signal.lfilter(num,den,x,zi=zi*ic) # y1[n]
y2,_ = signal.lfilter(num,den,xd,zi=zi*ic) # y2[n]

y2D = y2[D:] #计算输入为x[n-D]的响应的D个单位超前

# 计算输入为x[n]的响应与输入为x[n-D]的响应的D个单位超前之间的差
d = y1-y2D


plt.subplot(121)
plt.stem(n,y1)
plt.title('y1[n]')
plt.subplot(122)
plt.stem(n,d)
plt.title('Difference')
plt.show()

../_images/experiments_dt_systems_5_0.png

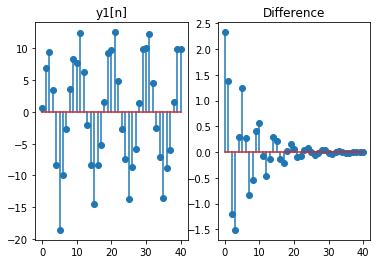
若上述系统的初始条件不等于0，系统还是时不变系统吗？

[4]:

ic = np.array([1,0]) # set initial
zi = signal.lfilter_zi(num, den)
y1,_ = signal.lfilter(num,den,x,zi=zi*ic) # y1[n]
y2,_ = signal.lfilter(num,den,xd,zi=zi*ic) # y2[n]

y2D = y2[D:] #计算输入为x[n-D]的响应的D个单位超前

# 计算输入为x[n]的响应与输入为x[n-D]的响应的D个单位超前之间的差
d = y1-y2D

plt.subplot(121)
plt.stem(n,y1)
plt.title('y1[n]')
plt.subplot(122)
plt.stem(n,d)
plt.title('Difference')
plt.show()

../_images/experiments_dt_systems_7_0.png

线性时不变系统、冲激响应和阶跃响应、卷积¶

线性时不变（LTI）系统既满足线性性质又满足时不变性质。

离散时间系统对单位样本序列\(\delta[n]\)的响应称为单位样本响应，或者冲激响应，用\(h[n]\)来表示。

有限冲激和无限冲激响应系统: 冲激响应序列\(h[n]\)的长度无限长时，称系统为无限冲激响应系统；冲激响应序列\(h[n]\)的长度有限长时，称系统为有限冲激响应系统。

离散时间系统对单位阶跃序列\(\mu[n]\)的响应称为单位阶跃响应，或者阶跃响应，用\(s[n]\)来表示。

离散时间系统输入信号\(x[n]\)时的输出响应\(y[n]\)，可以表示为冲激响应\(h[n]\)和输入信号\(x[n]\)的加权累加和

\[y [ n ] = \sum _ { k = - \infty } ^ { \infty } h [ k ] x [ n - k ]\]

通过简单的变量代换，也可表示为

\[y [ n ] = \sum _ { k = - \infty } ^ { \infty } h [ n - k ] x [ k ]\]

上述两个式子称为序列\(x[n]\)和\(h[n]\)的卷积和

\[y [ n ] = h [ n ] \circledast x [ n ]\]

其中符号\(\circledast\)表示卷积和。

[5]:

N = 40
# 定义系统的系数
num = np.array([2.2403,2.4908,2.2403])
den = np.array([1,-0.4,0.75])
dt = 1

# 系统的冲激响应
t, h = signal.dimpulse((num,den,dt),n=N)
t, s = signal.dstep((num,den,dt),n=N)
plt.subplot(121)
plt.plot(t,np.squeeze(h))
plt.subplot(122)
plt.plot(t,np.squeeze(s))
plt.show()

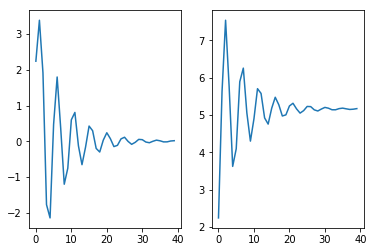
../_images/experiments_dt_systems_9_0.png

[6]:

# 系统的输出等于冲激响应序列和输入序列的卷积
n = np.linspace(0,40,41)
a = 2
b = -3
x = a*np.cos(2*np.pi*0.1*n)+b*np.cos(2*np.pi*0.4*n)

# 定义系统参数
num = np.array([2.2403,2.4908,2.2403])
den = np.array([1,0,0])#np.array([1,-0.4,0.75])

# 利用lfilter计算
ic = np.array([0,0]) # set initial
y1,_ = signal.lfilter(num,den,x,zi=ic) # y1[n]

# 利用卷积计算
t, h = signal.dimpulse((num,den,dt),n=41)

y2 = signal.convolve(x,np.squeeze(h))

plt.subplot(121)
plt.plot(n,y1)
plt.subplot(122)
plt.plot(y2[:41])
plt.show()

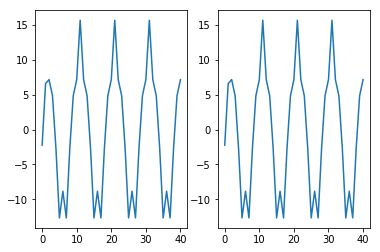
../_images/experiments_dt_systems_10_0.png

BIBO稳定¶

若对于任意有界输入序列\(x[n]\)，其输出\(y[n]\)也是一个有界序列，则该离散时间系统是有界输入有界输出（BIBO）稳定的，也就是说，若

\[|x[n]| < B_x,\forall n\]

则响应的输出\(y[n]\)也有界，即

\[|y[n]| < B_y,\forall n\]

当且仅当线性时不变离散时间系统的冲激响应序列\(h[n]\)绝对可和时，改线性时不变系统是BIBO稳定的，即

\[\sum _ { n = - \infty } ^ { \infty } | h [ n ] | < \infty\]

[7]:

# 定义系统参数
num = np.array([1,-0.8])
den = np.array([1,1.5,0.9])
# 冲激响应序列
t, h = signal.dimpulse((num,den,1),n=200)
h = np.squeeze(h)
N = 200
parsum = 0
for k in range(N):
    parsum = parsum + np.abs(h[k])
print(parsum)

# 画出冲激响应
plt.plot(t,h)
plt.show()

35.35909090875415

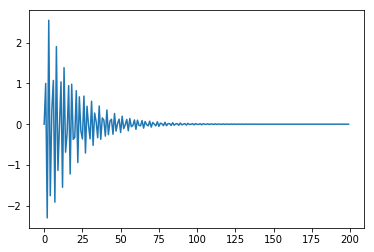
../_images/experiments_dt_systems_12_1.png

因果系统¶

若\(y_1[n]\) \(y_2[n]\)分别是因果离散时间系统输入信号\(u_1[n]\) \(u_2[n]\)的响应，则当

\[u _ { 1 } [ n ] = u _ { 2 } [ n ] \qquad n < N\]

时

\[y _ { 1 } [ n ] = y _ { 2 } [ n ] \qquad n < N\]

当且仅当线性时不变离散时间系统的冲激响应序列\(h[n]\)满足

\[h[k]=0, \qquad k < 0\]

该LTI离散时间系统才是因果的。

滤波概念的解释¶

考虑用如下差分方程描述的两个离散时间系统：

系统1¶

\[y [ n ] = 0.5 x [ n ] + 0.27 x [ n - 1 ] + 0.77 x [ n - 2 ]\]

系统2¶

\[y [ n ] = 0.45 x [ n ] + 0.5 x [ n - 1 ] + 0.45 x [ n - 2 ] + 0.53 y [ n - 1 ] - 0.46 y [ n - 2 ]\]

对输入

\[x [ n ] = \cos \left( \frac { 20 \pi n } { 256 } \right) + \cos \left( \frac { 200 \pi n } { 256 } \right) , \qquad 0 \leqslant n < 299\]

计算上述两个系统的输出。

[8]:

# 产生混合信号：高频正弦+低频正弦
n = np.linspace(0,299,300)
s1 = np.cos(2*np.pi*n/256*10)
s2 = np.cos(2*np.pi*n/256*100)
x = s1+s2

# 定义两个系统的系数
num1 = np.array([0.5,0.27,0.77])
den1 = np.array([1,0,0])
num2 = np.array([1,-0.53,0.46])
den2 = np.array([0.45,0.5,0.45])
# 系统处理（滤波）
ic = np.array([0,0]) # set initial
y1,_ = signal.lfilter(num1,den1,x,zi=ic) # y1[n]
y2,_ = signal.lfilter(num2,den2,x,zi=ic) # y2[n]


plt.subplot(311)
plt.plot(n,x)
plt.title('x[n]')
plt.subplot(312)
plt.plot(n,y1)
plt.title('y1[n]')
plt.subplot(313)
plt.plot(n,y2)
plt.title('y2[n]')
plt.show()

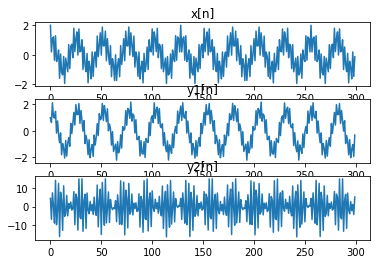
../_images/experiments_dt_systems_15_0.png

[ ]: