2.1. 时域中的离散时间信号

数字信号处理是处理一种称之为输入信号的离散时间信号,以产生另一种称之为输出信号的离散时间信号,这种输出信号具有更多人们所需要的性质.在某些应用中,需要使用特定的数字信号处理算法来提取原信号的一些重要性质.通过观察系统对给定输入信号的输出信号,还可以研究离散时间系统的特性.

因此,我们首先要学会用Python在时域中产生一些基本的离散时间信号,并对这些信号进行一些基本的运算.其次,学会使用基本的Python命令,并将它们应用到简单的数字信号处理问题中.

相关Python包

科学计算包

科学计算包Numpy作为基础包在后学学习数字信号处理过程中会大量使用,这里通过下面的命令可以加载到程序中.

import numpy as np

绘图包

绘图包Matplotlib包含大量的绘图工具,可以完成跟Matlab中plot函数相当的功能,因此后续学习过程中需要可视化最终结果时,会用到这个包中的函数.

import matplotlib.pyplot as plt

离散时间信号

离散时间信号由样本构成的数字序列来表示.典型的离散时间信号或者序列表示为

\[\{x[n]\}\]

其中\(x[n]\)为样本值,\(n\)为样本的序号(整数),取值范围为\(-\infty\sim \infty\).

一般,我们为了简便起见,将外面的花括号去掉.

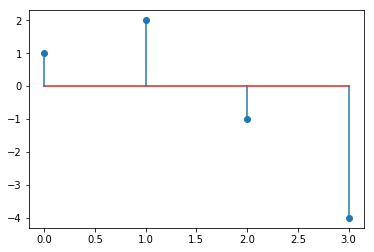
# 产生一个样本序列$x[n] = \{1,2,-1,-4\}$
import matplotlib.pyplot as plt
import numpy as np

n = np.linspace(0,3,4) # 定义序号
xn = [1,2,-1,-4] # 定义序列
plt.stem(n,xn)   # 画出序列图形

print(xn)      # 显示序列

[1, 2, -1, -4]

序列的能量和平均功率

序列\(x[n]\)的能量定义为

\[\mathcal{E} = \sum_{n=-\infty}^\infty |x[n]|^2\]

有限长度序列的能量定义为

\[\mathcal{E}_K = \sum_{n=-K}^K |x[n]|^2\]

非周期信号\(x[n]\)的平均功率定义为

\[\mathcal{P}_{av} = \lim_{K\to \infty} \frac{1}{2K+1} \mathcal{E}_K = \lim_{K\to \infty} \frac{1}{2K+1} \sum_{n=-K}^K |x[n]|^2\]

周期信号\(\tilde{x}[n]\)的平均功率为

\[\mathcal{P}_{av} = \frac{1}{N} \sum_{n=0}^{N-1}|\tilde{x}[n]|^2\]

# 计算给定序列的能量
n = np.linspace(0,3,4) # 定义序号
xn = np.sin(2*np.pi*0.2*n)
E = np.sum(xn**2)   # 序列的能量
print('信号x[n]的能量为E=%.3f' % E)

信号x[n]的能量为E=1.595

# 计算周期正弦序列的平均功率
n = np.linspace(0,4,5) # 定义序号
xn = np.sin(2*np.pi*0.2*n) # 周期为5的正弦序列
P = np.sum(xn**2)/5   # 序列的能量
print('信号x[n]的平均功率为P=%.3f' % P)

信号x[n]的平均功率为P=0.500

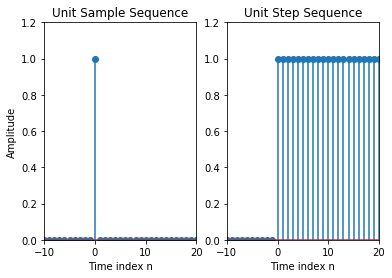
单位样本序列和单位阶跃序列

单位样本序列(或者离散时间沖激或单位沖激),用\(\delta[n]\)来表示,其定义为

\[\begin{split}\delta[n] = \begin{cases} 1, & \quad n=0 \\ 0, & \quad n\neq 0 \end{cases}\end{split}\]

单位阶跃序列用\(\mu[n]\)来表示,定义为

\[\begin{split}\mu[n] = \begin{cases} 1, & \quad n\geq 0 \\ 0, & \quad n< 0 \end{cases}\end{split}\]

n = np.arange(-10,21,1)
hn = np.concatenate((np.zeros([1,10]),np.ones([1,1]),np.zeros([1,20])),axis=1)#,np.zeros([1,20]))
un = np.concatenate((np.zeros([1,10]),np.ones([1,21])),axis=1)

plt.subplot(121)
plt.stem(n,hn.transpose())
plt.xlabel('Time index n')
plt.ylabel('Amplitude')
plt.title('Unit Sample Sequence')
plt.axis([-10,20,0,1.2])

plt.subplot(122)
plt.stem(n,un.transpose())
plt.xlabel('Time index n')
plt.title('Unit Step Sequence')
plt.axis([-10,20,0,1.2])
plt.show()

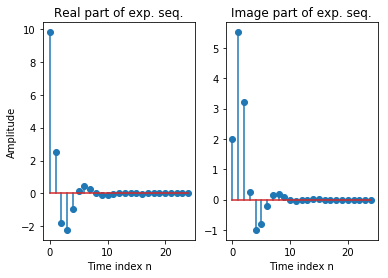
指数序列

指数序列定义为

\[x[n] = A \alpha ^n\]

其中,\(A\)和\(\alpha\)是任意的实数或者复数,表示为

\[\alpha = e^{\sigma_0+j\omega_0} \quad A = |A|e^{j\phi}\]

所以指数序列还可以改写为

\[x[n] = |A|e^{\sigma_0 n+ j(\omega_0n + \phi)} = |A|e^{\sigma_0n}(\cos(\omega_0n + \phi)+j\sin(\omega_0n + \phi))\]

# 产生一个指数序列:sigma=-0.5,w0=0.15,phi=0.2,|A|=10
n = np.linspace(0,24,25) # 定义序号
w0=0.15
phi=0.2
A=10
sigma=-0.5
en = A*np.exp(sigma*n+1j*(2*np.pi*n*w0+phi))

plt.subplot(121)
plt.stem(n,en.real)
plt.xlabel('Time index n')
plt.ylabel('Amplitude')
plt.title('Real part of exp. seq.')
plt.subplot(122)
plt.stem(n,en.imag)
plt.xlabel('Time index n')
plt.title('Image part of exp. seq.')
plt.show()

正弦序列及其周期性

正弦序列定义为

\[x[n] = |A|\cos(\omega_0n + \phi)\]

式子中的\(|A|\),\(\omega_0\)和\(\phi\)分别被称为正弦序列的幅度,角频率和相位.

若\(\omega_0N\)为\(2\pi\)的整数倍,当\(\sigma_0=0\)时,复指数序列和正弦序列都是周期序列,此时周期为满足条件的最小的\(N\)

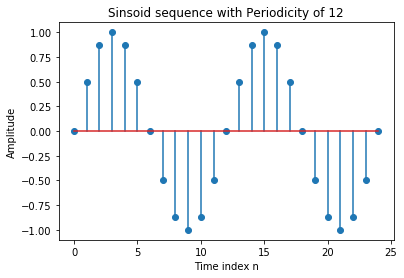
# 产生一个周期为12的正弦序列
n = np.linspace(0,24,25) # 定义序号
xn = np.sin(2*np.pi*n/12)
plt.stem(n,xn)
plt.xlabel('Time index n')
plt.ylabel('Amplitude')
plt.title('Sinsoid sequence with Periodicity of 12')
plt.show()

序列的基本运算

长度为N的两个序列\(x[n]\)和\(h[n]\)的乘积,产生长度为N的序列\(y[n]\)

\[y[n]=x[n] \cdot h[n]\]

长度为N的两个序列\(x[n]\)和\(h[n]\)的相加,产生长度为N的序列\(y[n]\)

\[y[n]=x[n] + h[n]\]

标量A和长度为N的序列\(x[n]\)相乘,产生长度为N的序列\(y[n]\)

\[y[n]=A\cdot x[n]\]

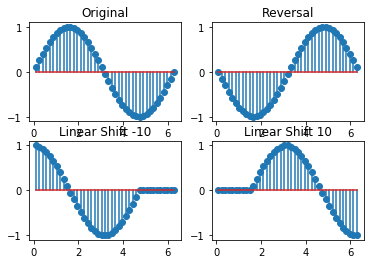
无限长序列\(x[n]\)通过时间翻转,得到无限长序列\(y[n]\)

\[y[n]=x[-n]\]

无限长序列\(x[n]\)通过时间延迟(超前),得到无限长序列\(y[n]\)

\[y[n] = x[n-m]\]

长度为N的序列\(x[n]\),可以被长度为M的序列\(g[n]\)扩充,得到长度为\(N+M\)的序列\(y[n]\)

\[\{y[n]\} = \{\{x[n]\},\{g[n]\}\}\]

# 循环平移函数
x = np.linspace(0.1, 2 * np.pi, 41)
y1 = np.sin(x)
y2 = np.cos(2*x)
def cshift(key,array):
    return np.append(array[-key:],array[:-key])

# 线性平移

def lshift(key,array):
    if key<0:
        return np.append(array[-key:],np.zeros([-key]))
    else:
        return np.append(np.zeros([key]),array[:-key])

ylr = np.flipud(y1)     # flip left and right
yls = lshift(-10,y1)    # left shift
yrs = lshift(10,y1)     # right shift

plt.subplot(221)
plt.title('Original')
plt.stem(x, y1)
plt.subplot(222)
plt.title('Reversal')
plt.stem(x, ylr)
plt.subplot(223)
plt.title('Linear Shift -10')
plt.stem(x, yls)
plt.subplot(224)
plt.title('Linear Shift 10')
plt.stem(x, yrs)
plt.show()

例子: 信号平滑

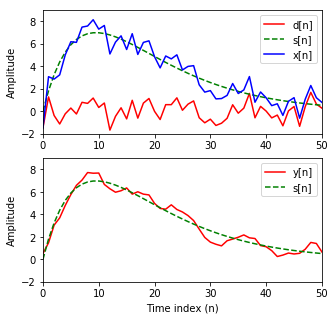
数字信号处理应用的一个常见的例子就是从被加性噪声污染的信号中移除噪声.假定信号\(s[n]\)被噪声\(d[n]\)污染,得到了一个含有噪声的信号

\[x[n] = s[n] +d[n]\]

我们的目的是对\(x[n]\)进行计算,产生一个合理的逼近\(s[n]\)的信号\(y[n]\).因此,对时刻\(n\)的样本附近的样本求平均,产生输出信号是一种简单有效的方法,例如三点滑动平均

\[y[n] = \frac{1}{3}(x[n-1]+x[n]+x[n+1])\]

# 通过滑动平均平滑信号
R = 51
d = .8*np.random.normal(0,1,[R,])
n = np.arange(0,R,1)

s = 2*n*(0.9**n)
x = s+d

x1 = np.concatenate((np.zeros([2,]),x),axis=0)
x2 = np.concatenate((np.zeros([1,]),x,np.zeros([1,])),axis=0)
x3 = np.concatenate((x,np.zeros([2,])),axis=0)
# Average
y1 = (x1+x2+x3)/3
y = y1[1:-1]

# 绘制结果
fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(211)
ax.plot(n,d,'r-',label='d[n]')
ax.plot(n,s,'g--',label='s[n]')
ax.plot(n,x,'b-',label='x[n]')
ax.axis([0,50,-2,9])
plt.legend(loc='upper right')
plt.ylabel('Amplitude')

ax = fig.add_subplot(212)
ax.plot(n,y,'r-',label='y[n]')
ax.plot(n,s,'g--',label='s[n]')
ax.axis([0,50,-2,9])
plt.legend(loc='upper right')
plt.xlabel('Time index (n)')
plt.ylabel('Amplitude')

plt.show()