3. 卷积和相关

3.1. 卷积

两个序列卷积的定义

\[y[n] = x[n] \circledast h[n] \triangleq \sum_{k=-\infty}^\infty x[k] h[n-k]\]

它的计算过程可以分解为如下四个步骤： 1. 翻转 2. 移位 3. 相乘 4. 求和

那么，可以根据定义编写如下卷积计算的Matlab函数。

function conv_dsp(x,y)
lx = length(x);
ly = length(y);
M = lx+ly-1;

x = [flipud(x(:));zeros(M,1)]; % 翻转
y = [y(:);zeros(lx-1,1)];

z = zeros(M,1);

for i = 1:M
    xshift = wshift('1d',x,-i); % 移位
    z(i) = sum(y.*xshift(lx+1:end)); %相乘求和
end
end

x = [1,0,2,1,0,0,1]
y = [2,0,1]
z1 = conv_dsp(x,y)
z2 = conv_dsp(y,x)

x =

     1     0     2     1     0     0     1


y =

     2     0     1


z1 =

     2
     0
     5
     2
     2
     1
     2
     0
     1


z2 =

     2
     0
     5
     2
     2
     1
     2
     0
     1

手算卷积的话，直接通过公式实际上不是很方便，而且很容易出错。我们还可以通过表格法来计算卷积。表格法计算方法，主要分为下面 若两个序列长度分别为\(M\)和\(N\)，那么

1. 构造\(M\times N\)的表格

2. 将表格的两个方向的第一行和第一列分别填入对应序列的每个元素值

3. 对应交叉位置相乘，将乘积填入表格中

4. 将表格中反斜对角上的所有元素相加，分别就能得到对应位置卷积的结果

例如序列\(x[n]=\{1,0,2,1,0,0,1\}\)和序列\(y[n]=\{2,0,1\}\)的卷积和按照表格法计算如下：

经过求和之后，得到最后的卷积结果为

\[x[n] \circledast y[n] = [2,0,5,2,2,1,2,0,1]\]

3.1.1. 卷积的性质

与Dirac函数的卷积:

\[x[n]\circledast k\delta[n+\tau]=kx[n+\tau]\]

交换律:

\[x[n]\circledast h[n] = h[n] \circledast x[n]\]

结合律:

\[x[n]\circledast h_1[n] \circledast h_2[n] =x[n] \circledast (h_1[n]\circledast h_2[n])\]

分配律:

\[x[n] \circledast (h_1[n]+h_2[n])=x[n]\circledast h_1[n] + x[n] \circledast h_2[n]\]

3.1.2. 卷积的物理意义

1. 信号合成的角度（与Dirac序列卷积）

2. 信号分析的角度（与特定信号卷积）

3.2. 相关

对于两个序列\(x[n],h[n]\in \mathbb{C}\)

1. 互相关序列

\[r_{xh}[n] \triangleq \sum^{\infty}_{k=-\infty}x[k]h^*[{ k+n}]\]

2. 自相关序列

\[r_{x}[n] \triangleq \sum^{\infty}_{k=-\infty}x[k]x^*[{ k+n}]\]

3.2.1. 卷积与相关的关系

1. 相关运算

\[z[n]=r_{xh}[n] = \sum^{\infty}_{k=-\infty}x[k]h^{\color{red} *}[n{\color{red} +k}]\]

2. 卷积运算

\[y[n]=x[n]\circledast h[n] = \sum^{\infty}_{k=-\infty}x[k]h[n{\color{red} -k}]\]

相似之处：

1. 卷积等于相关，但是是对\(h[-n]\)做相关；

2. 当序列\(h[n]\)是共轭对称序列时，卷积与相关完全等价。

不同之处：

1. 卷积满足交换律，但是相关不满足；

2. 卷积描述了LTI系统的行为，但是相关描述了两个信号之间的相似性。

3.2.2. 利用相关性

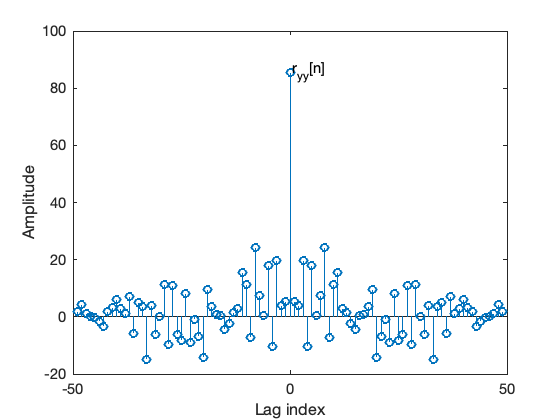
利用rand产生一个均匀分布的随机信号，并加到一实指数序列\(e^{-0.8 n}\)上，计算此受干扰序列的自相关序列，证明受干扰序列的自相关序列在零延时处呈现一个尖峰。

N = 50;
n = 0:N-1;
x = exp(-0.8*n);
y = randn(1,N)+x;
n1 = length(x)-1;
r = conv(y,fliplr(y)); % 利用卷积计算相关，这里需要将第二个参数翻转。
k = (-n1):n1;
stem(k,r);
xlabel('Lag index');ylabel('Amplitude');
gtext('r_{yy}[n]');