基于傅里叶变换的自动对焦算法

利用收集的手动拍摄功能,手动调整相机的焦距,得到焦距从1毫米到90毫米,一共10张照片. 可以发现,这些照片从不清晰变成清晰,然后又变为不清晰.

可以发现,这10张照片中,当焦距为40和50毫米的时候,拍摄的照片最清晰.

那么如何设计一个算法,来自动找到合适的焦距呢?

原理介绍

对焦正确，拍摄的照片具有如下特征： 1. 边缘清晰 2. 纹理丰富

清晰的边缘就表示陡峭的变化，丰富的纹理表示重复周期变化的信号。因此，这两种特征都表示该图像的高频成分比较丰富，也就是高频部分的能量比较高。

如果对焦不正确，拍摄的照片则正好相反：边缘模糊、纹理模糊，整个图像上变化比较平坦，因此该图像的低频成分比较丰富。

所以，通过高频部分能量是否达到最大值，我们就能很容易的判断这幅图像是否对焦正确。

二维图像傅里叶变换

二维傅里叶变换（连续）公式如下：

\[F(u, v)=\iint_{-\infty}^{\infty} f(x, y) e^{-j 2 \pi(u x+\nu y)} d x d y\]

其中 \(u,v\)为频域的两个维度，\(x,y\)为空域的两个维度。

在 Matlab 中，我们可以通过调用fft2来计算二维图像的傅里叶变换。

% 读入第一幅图像，并且将其转换为灰度图
I = imread(['u',num2str(1),'.jpg']);
Ig = double(rgb2gray(I));
imshow(Ig,[])

% 对该图像进行二维傅里叶变换，对数显示
I_freq = fftshift((abs(fft2(Ig))));
imshow(log(I_freq+eps),[0,20])

计算频域中高频成分能量

假设频谱图中中心区域[-128,128,-90,90]范围内是图像的低频部分，那么高频成分能量就是减去这部分低频成分能量之后的值。

c = [256,192]; % 图像中心点位置
I_freq(c(1)-128:c(1)+128,c(2)-90:c(2)+90) = 0;
e_high = sum(I_freq(:).^2);
disp('Energy of High Frequency:')
disp(e_high)

Energy of High Frequency:
   7.6148e+10

然后计算每一张在不同焦距条件下拍摄的照片的高频能量：

f = [1,10,20,30,40,50,60,70,80,90];% 焦距列表
e_high = zeros(length(f),1);
for i=1:10
    I = imread(['u',num2str(i),'.jpg']);
    Ig = rgb2gray(I);
    I_freq = fftshift((abs(fft2(Ig))));
    I_freq(c(1)-128:c(1)+128,c(2)-90:c(2)+90) = 0;
    e_high(i) = sum(I_freq(:).^2);
end

% 显示部分
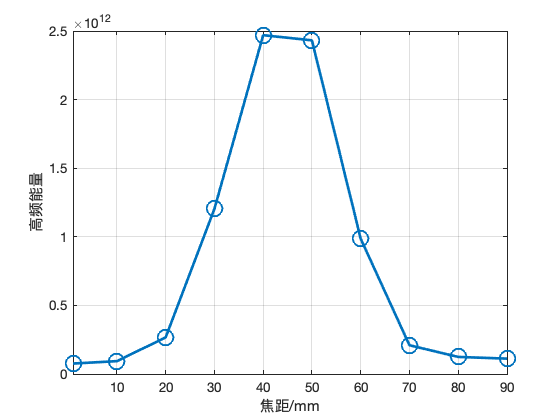
plot(f,e_high,'-o','linewidth',2,'markersize',12);
axis([1,90,0,2.5e12]);
xlabel('焦距/mm')
ylabel('高频能量')
grid on