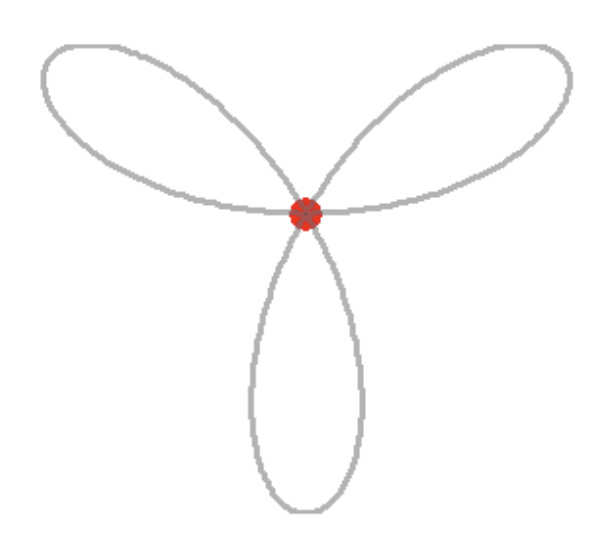
3. 数据和函数的可视化¶
(右键点击如下链接,另存为.p文件)
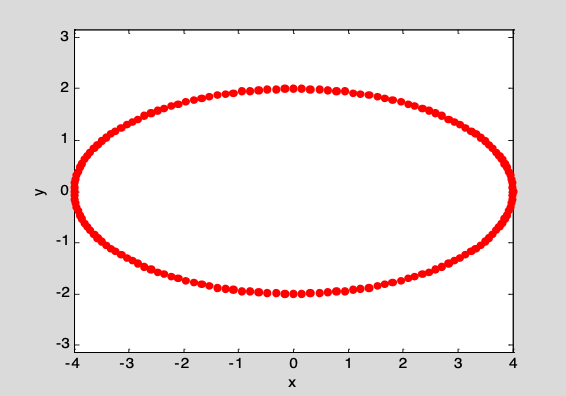
1. 已知椭圆的长、短轴$a=4,b=2$,用“小红点线”画如图所示的椭圆$\begin{cases}
x&=a \cos t \\
y&=b \sin t
\end{cases}$。(提示:参量$t$ ;点的大小; axis equal)
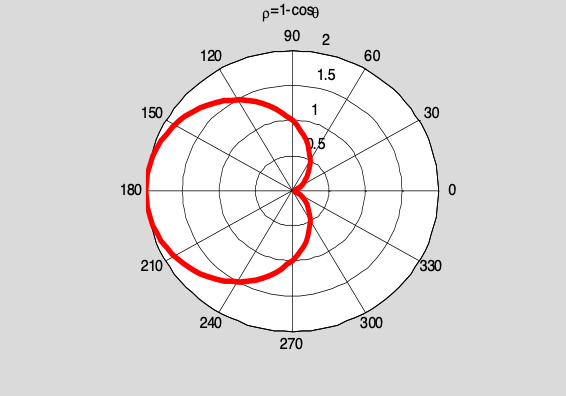
2. 根据表达式$\rho = 1-\cos \theta$ 绘制如图的心脏线。(提示:polar;注意title中特殊字符;线宽;axis square。可以用plot试试。)
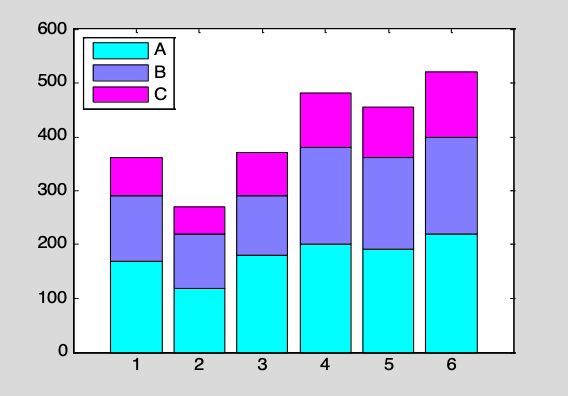
3. A,B,C三个城市上半年每个月的国民生产总值表。试画出如图所示的三城市上半年每月生产总值的累计直方图。(提示:bar(x,Y,'style'); colormap(cool); legend。)
表 各城市生产总值数据(单位:亿元)
| 城市 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
|---|---|---|---|---|---|---|
| A | 170 | 120 | 180 | 200 | 190 | 220 |
| B | 120 | 100 | 110 | 180 | 170 | 180 |
| C | 70 | 50 | 80 | 100 | 95 | 120 |
4. 二阶线性系统的归一化(即令 $\omega_n=1$)冲激响应可表示为:
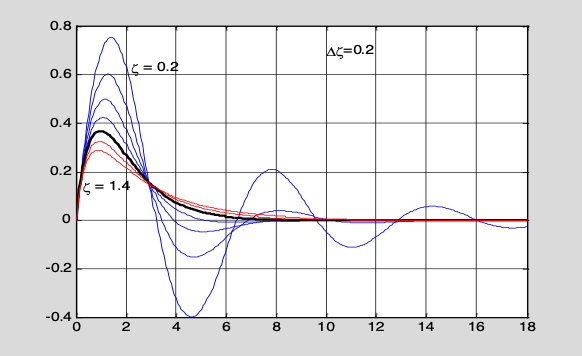
,其中$\beta=\sqrt{|1-\xi^2|}$, $\xi$为阻尼系数。(1)希望在同一张图上,绘制$t\in [0,18]$区间内$\xi=0.2:0.2:1.4$不同取值时的各条曲线(参见下图)。在此图上,$\xi <1$的各条曲线为细蓝线; $\xi = 1$为粗黑线;$\xi>1$为细红线;并且对最上方及最下方的两条曲线给出$\xi=0.2$和$\xi=1.4$的醒目标志。(2)读者运行题下程序exmp504.m,可以发现该程序画出的曲线中没有“粗黑线”。你能讲出原因吗?如何对exmp504.m作最少的修改(比如只改一条指令),就可画出所需图形。(提示:该题深层次地暴露数值计算可能存在的隐患。)
% exmp504.m 供第4道习题使用的程序
clc,clf,clear;
t=(0:0.05:18)';
N=length(t);
zeta=0.2:0.2:1.4;
L=length(zeta);
y=zeros(N,L);
hold on
for k=1:L
zk=zeta(k);
beta=sqrt(abs(1-zk^2));
if zk<1 %满足此条件,绘蓝色线
y=1/beta*exp(-zk*t).*sin(beta*t);
plot(t,y,'b')
if zk<0.4
text(2.2,0.63,'\zeta = 0.2')
end
elseif zk==1 %满足此条件,绘黑色线
y=t.*exp(-t);
plot(t,y,'k','LineWidth',2)
else %其余,绘红色线
y=(exp(-(zk-beta)*t)-exp(-(zk+beta)*t))/(2*beta);
plot(t,y,'r')
if zk>1.2
text(0.3,0.14,'\zeta = 1.4')
end
end
end
text(10,0.7,'\Delta\zeta=0.2')
axis([0,18,-0.4,0.8])
hold off
box on
grid on
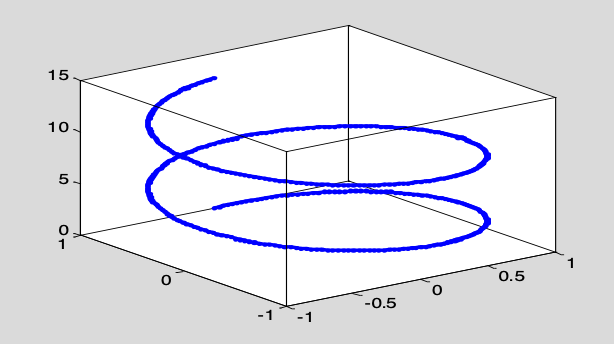
5. 用绿实线绘制$x=\sin(t),y=\cos(t),z=t$的三维曲线,曲线如图所示。(提示:参变量;plot3;线色线粗。)
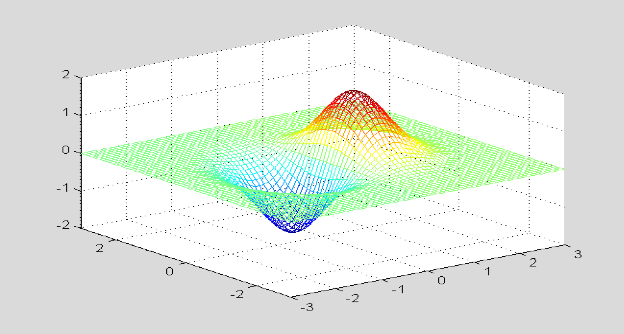
6. 采用两种不同方法绘制$z=4xe^{-x^2-y^2}$在$x,y\in [-3,3]$的如图的三维(透视)网格曲面。(提示:ezmesh; mesh; hidden)
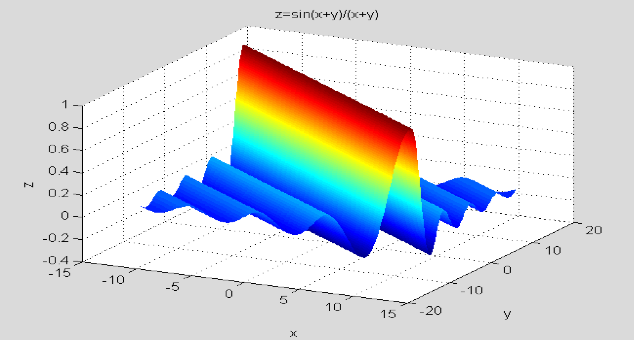
7. 在$x,y\in [-4\pi,4\pi]$区间里,根据表达式$z=\frac{\sin (x+y)}{x+y}$,绘制如图所示的曲面。(提示:NaN的处理)
8. 试用图解法回答:
a) 方程组$\begin{cases}
\frac{y}{1+x^2+y^2}=0.1 \\
\sin(x+\cos(y))=0
\end{cases}$有多少个实数解?(提示:图解法; ezplot; ginput)
b) 求出离$x=0,y=0$最近、且满足该方程组的一个近似解。
9. 制作如文件prob509.p(在光盘的mfiles文件夹上)运行时那样的色图变幻(参见图p5-8)。(提示:[jet; flipud(jet)]; colormap; spinmap)
10. 在$[0,4\pi]$区间内,根据$y(t,x)=e^{-0.2x}\sin(\frac{\pi}{24}t - x)$,通过如图所示曲线表现“行波”。做题前,请先运行prob510.p文件,观察演示。(提示:采用实时动画;使用两个line对象;background擦除模式;使用pause控制动画速度。)
11. 利用影片动画法,据函数$f(x,t)=\sin(x)\sin(t)$制作如图所示驻波动画。在做题前,先运行prob511.p产生的演示动画。(提示:用2个line分别产生带图柄的线和点对象; 擦除模式为background; 用set通过线图柄操作线位置; getframe; movie)
12. 编写使红色小球沿三叶线$\rho=\cos(3\theta)$运动的程序。具体参见演示程序prob512.p(在光盘的mfiles文件夹上)的运行实况。下图显示的是该动画中的一个静止图形。(提示:用参量方程表达三叶线;用line绘制线对象;用line创建红点的图柄,擦除模式用xor;用set操作红点坐标,构成动画;drawnow。)